JOURNAL OF CHILEAN CHEMICAL SOCIETY

Vol 63 No 3 (2018): Journal of the Chilean Chemical Society
Original Research Papers

COEFFICIENT PARTITION PREDICTION OF SATURATED MONOCARBOXYLIC ACIDS USING THE MOLECULAR DESCRIPTORS

PDF
  • Fahimeh Mohammaei,
  • Esmat Mohammadinasab
Fahimeh Mohammaei
Department of Chemistry, Arak Branch, Islamic Azad University
Esmat Mohammadinasab
Department of Chemistry, Arak Branch, Islamic Azad University
Published September 12, 2018
Keywords
  • Octanol-Water Coefficient Partition,
  • MLR Method,
  • Saturated Monocarboxilic Acid
How to Cite
Mohammaei, F., & Mohammadinasab, E. (2018). COEFFICIENT PARTITION PREDICTION OF SATURATED MONOCARBOXYLIC ACIDS USING THE MOLECULAR DESCRIPTORS. Journal of the Chilean Chemical Society, 63(3). Retrieved from https://jcchems.com/index.php/JCCHEMS/article/view/765

Copyright (c) 2018 Journal of the Chilean Chemical Society

Creative Commons License

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.

Abstract

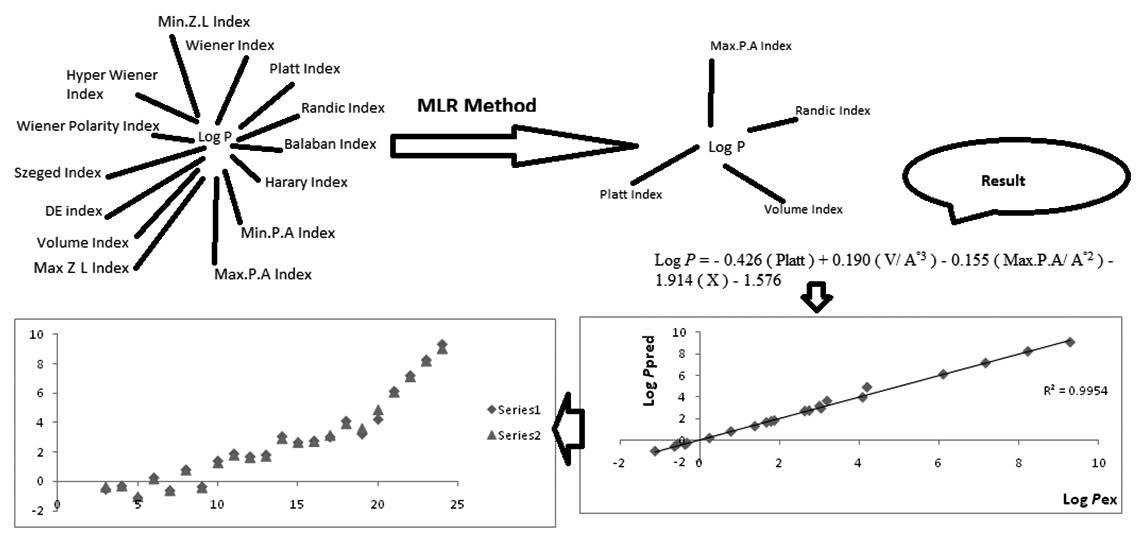
Carboxylic acids have clearly been absent from the quantitative structure-property relationship literature. The studies of the quantitative structure–property relationships (QSPR) involve various chemometric methods in which the physico-chemical behavior of a compound is correlated with its structure represented by the structural indices. For example, QSPR methods are applied for the prediction of octanol-water partition coefficient of an organic compound. In this study, the relationship between the octanol/water coefficient partition and molecular descriptors was investigated. Also, the multiple linear-regression method based on QSPR methodology was applied to predict the Log P of saturated mono-carboxylic acids C1-C22. On the other hand, the relation [ Log P = - 0.426 ( Platt ) + 0.190 ( V/ A°3 ) - 0.155 ( Max.P.A/ A°2 ) - 1.914 ( X ) - 1.576 ; N = 22, R2 = 0.995 , F = 917.005, DW=1.391] was generated for selected mono-carboxylic acids. The results of study indicated that the Platt, Randic, Volume and Maximum-Projection-Area descriptors have an important role in predicting the octanol/water coefficient partition of saturated monocarboxylic acids (C1- C22).

PDF

References

  1. W. Riemenschneider, Carboxylic Acids, Aliphatic, Ullmann’s Encyclopedia of Industrial Chemistry. Weinheim: Wiley-VCH, 2002.
  2. J. March, Advanced organic chemistry—reactions, mechanisms and structure. 4th edn, Wiley Interscience, New York, 8, 1992.
  3. J. R. Seward, T. W. Schultz, QSAR analyses of the toxicity of aliphatic carboxylic acids and salts to Tetrahymena pyriformis. SAR QSAR Environ Res. 10, 557, (1999).
  4. S. P. Torres, J. Sales, M. Rosés, C. Ràfols, E. Bosch , Journal of Chromatography A., 1217 (18), 3026, (2010).
  5. R. Smith and C. Tanford, Proc. Nat. Acad. Sci. USA, 70, (2), 289, (1973).
  6. F. Spafiu, A. Mischie, P. Ionita, A. Beteringhe, T. Constantinescu and A. T. Balabanb,. Arkivoc, General Papers, (x) 174, (2009).
  7. J. Devillers, A. T. Balaban, Topological indices and related descriptors in QSAR and QSPR. Gordon and Breach Science, Netherlands, 1999.
  8. E. Mohammadinasab, and M. Goodarzi, J. Fullerenes, Nanotubes, and Carbon Nanostructures., 19, 550, (2011).
  9. M. Goodarzi, E. Mohammadinasab, Fullerenes, Nanotubes and Carbon Nanostructures. 21, 2 ,102 (2013).
  10. M. Zanoozi and Z. Bayat, Pelagia Research Library, Der Chemica Sinica. 2(6), 288. (2011).
  11. Z. Bayat, J. Movaffagh, Russian Journal of Physical Chemistry A. 84, (13), 2293, (2010).
  13. G.W. Snedecor, W. G. Cochran, Statistical methods, Oxford and IBH, New Delhi, 1967.
  14. S. Wold, M. Sjöström, L. Eriksson. Chemometrics and Intelligent Laboratory Systems, 58, 109, (2001).
  15. A. Agresti, An introduction to categorical data analysis, Wiley, Hoboken, 1996.
  16. J. G. Topliss, R. J. Costello, J. Med Chem. 15, 1066, (1972).
  17. I. Gutman and O.E. Polansky, Mathematical Concepts in Organic Chemistry, Springer-Verlag, Berlin, 1986.
  18. R. Todeschini, V. Consonni, Handbook of Molecular Descriptors, Methods and Principles in Medicinal Chemistry, WILEY-VCH Verlag GmbH, 2008.
  19. I. Gutman, B. Furtula(eds), novel molecular structure descriptors-theory and applications I and II, University of Kragujevac and Faculty of Science Kragujevac, 2010.
  20. J. Sangster, Octanol-Water Partition Coefficients of Simple Organic Compounds, J. Phys. Chem. Ref. Data. 18, 3, (1989).
  21. H. Wiener, J. Am. Chem. Soc. 69, 17, (1947).
  22. G. Cash, S. Klavzar, Marko Petkovsek, J. Chem. Inf. Comput. Sci. 42, 571, (2002).
  23. X. Li, Y. Shi, MATCH Communications in Mathematical and in Computer Chemistry. 59 (1) 127, (2008).
  24. M. Randic, MATCH Commun. Math. Comput. Chem. 7, 5, (1979).
  25. B. Liu, I. Gutman, MATCH Communications in Mathematical and in Computer Chemistry., 58 (1), 147, (2007).
  26. M. Randic, J. Am. Chem. 97(23), 6609, (1975).
  27. A. T. Balaban and T. S. Balaban, Math. Chem. 8, 383, (1991).
  28. K. C. Das, B. Zhou and N. TrinajstiQ, J. Math. Chem. 1369, (2009).
  29. I. Gutman, Graph Theory Notes of New York. 27, 9, 1994.
  30. P. V. Khadikar, N. Deshpande, P. P. Dobrynin, J. Chem. Inf. Compt. Sci.35, 547 (1995).
  31. Web search engine developed by ChemAxon; software available at, http:// WWW. Chemicalize. Org.

Copyright @2019 | Designed by: Open Journal Systems Chile Logo Open Journal Systems Chile Support OJS, training, DOI, Indexing, Hosting OJS

Code under GNU license: OJS PKP